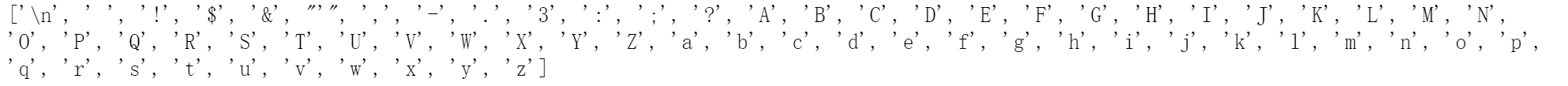|
|
преди 2 години | |
|---|---|---|
| LSTM final.ipynb | преди 2 години | |
| README.md | преди 2 години | |
| model.h5 | преди 2 години | |
| shakespeare.txt | преди 2 години |
README.md
LSTM模型预测文本序列
神经网络基础概念
参考资料: 3Blue1Brown深度学习
神经网络的基本结构与前向传播
基本结构
神经网络,顾名思义源自人的大脑结构,但不同于生物学上的神经细胞的二元状态(激活/未激活),深度学习中的神经元是一个连续的数字
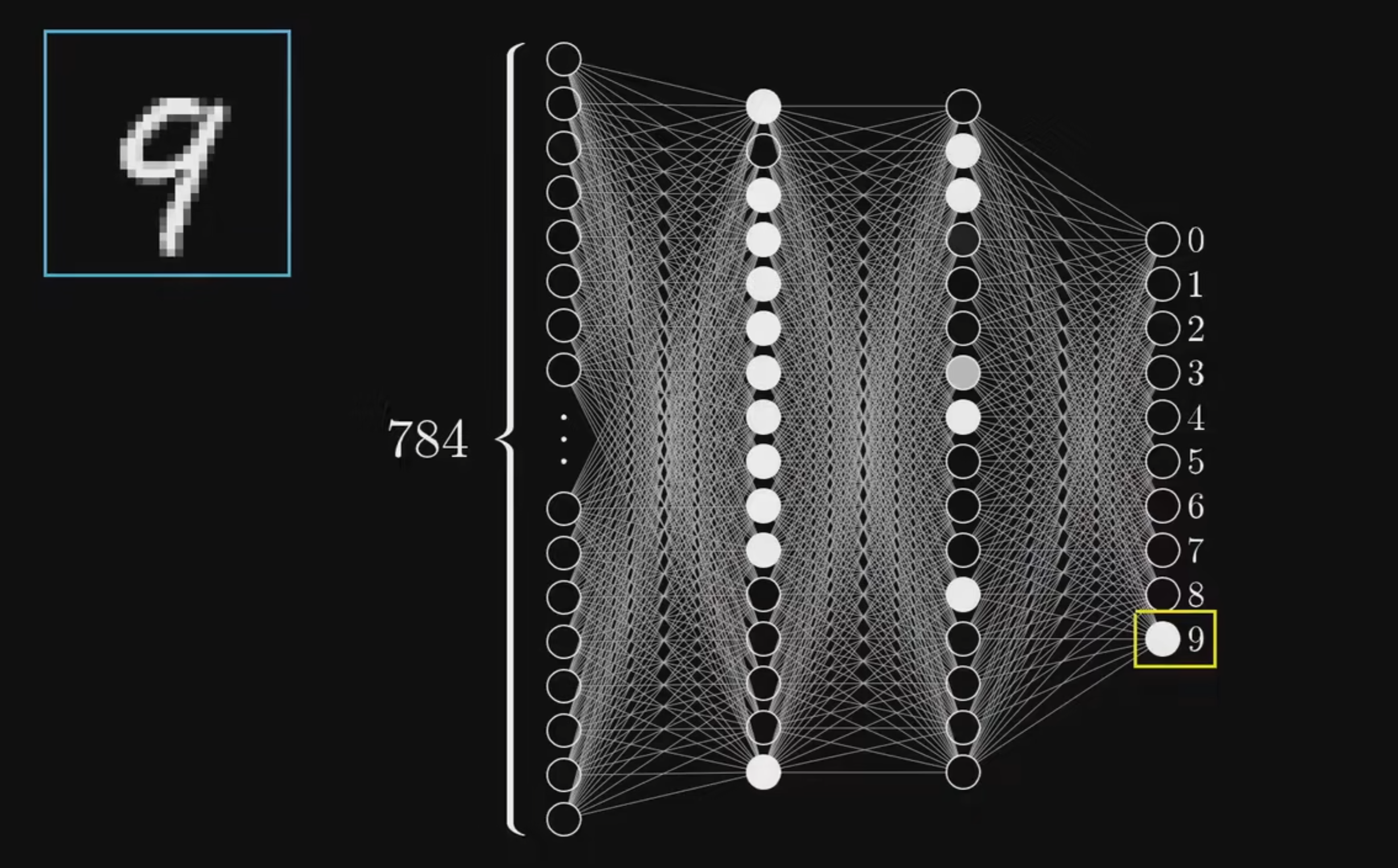
在下面的任务中,需要识别28x28像素的手写数字图片;如图,每个像素的灰度值即可代表第一层输入层的神经元
将28x28的图片像素平铺后,即可得到784个输入层神经元,如下图
在上面的模型中,可以看到,除了784个神经元组成的输入层,以及最右侧10个神经元组成的输出层(神经元的值越大,则代表模型预测图片对应该数字的可能性越大),中间还有两个16个神经元组成的隐含层。
为什么要加入两个隐含层呢,以及为什么要将其设置为16个神经元呢?这里可以简单地理解为隐含层处理了识别数字的子任务(例如:识别横、竖、圆等,虽然实际上并非如此,因为场景有限机器并没有像人脑识别世界一样去学习,而是收敛到了一个相对稳定能完成识别任务的区域),因此这里的隐含层的设置其实有很多可以设置的空间。
而每一层神经元互相连接的线,就是前向传播与反向传播的通道,代表了两层神经元之间的关系。
前向传播
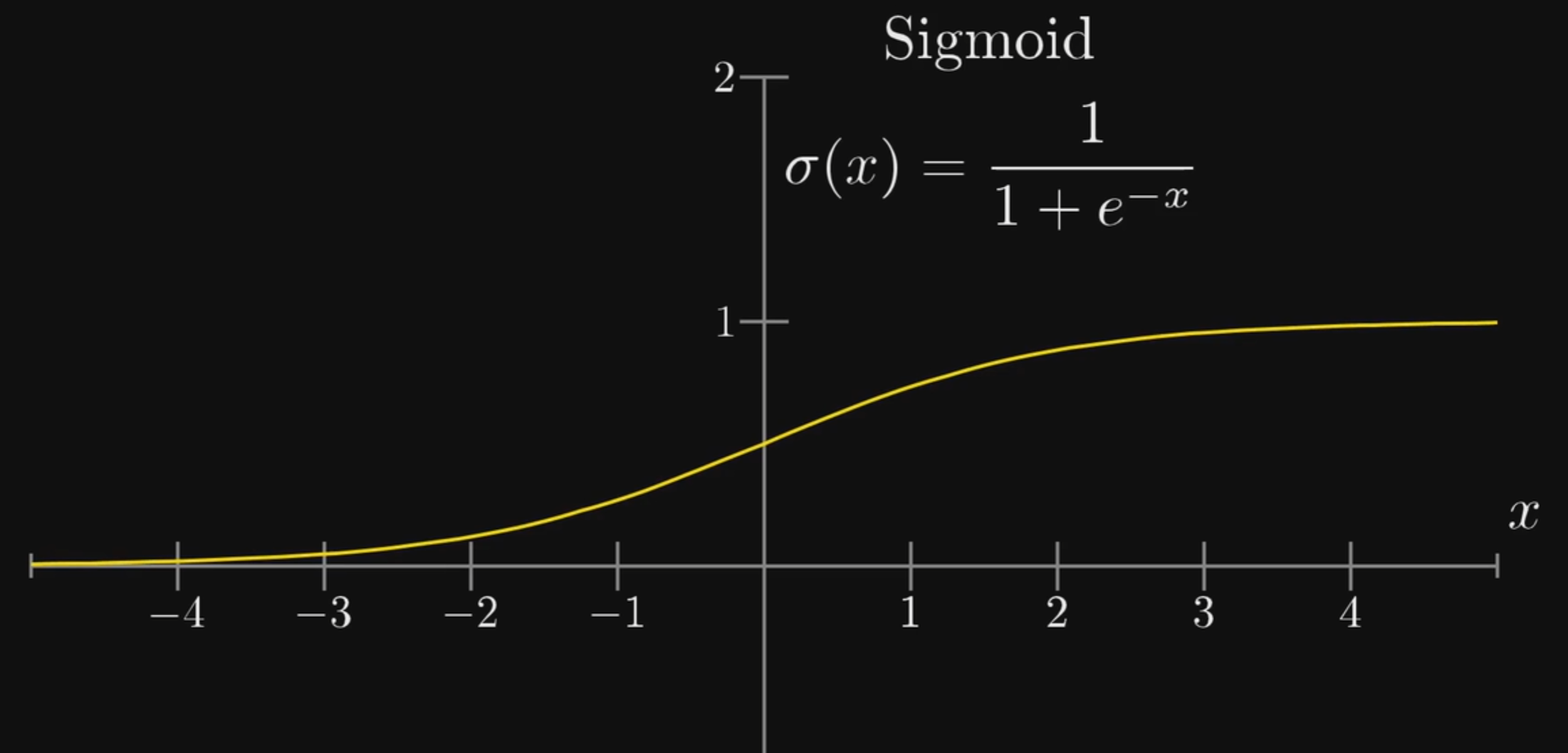
其中,每条线包含了一个权重值,数学上的表示为: $$ 设第一层神经元为a_1^{(0)}、a_2^{(0)}、a_3^{(0)}、a_4^{(0)}...\ 第二层神经元为a_1^{(1)}、a_2^{(1)}、a_3^{(1)}、a4^{(1)}...\ 两层之间的连接为w{11}、w_{21}...\ 则计算a_1^{(1)}时:a1^{(1)}=sigmoid(w{11}a1^{(0)}+w{21}a2^{(0)}+w{31}a_3^{(0)}+...+bias) $$ 其中sigmoid函数用于对结果进行归一化(因为最终得到的结果应该是神经元的值,而神经元的值在0-1之间),其函数图像如下:
而bias是偏置,目的是改变权重与输入相乘所得结果的范围,能够表明此神经元是否更容易被激活
将上述数学表达式换为矩阵表达如下:
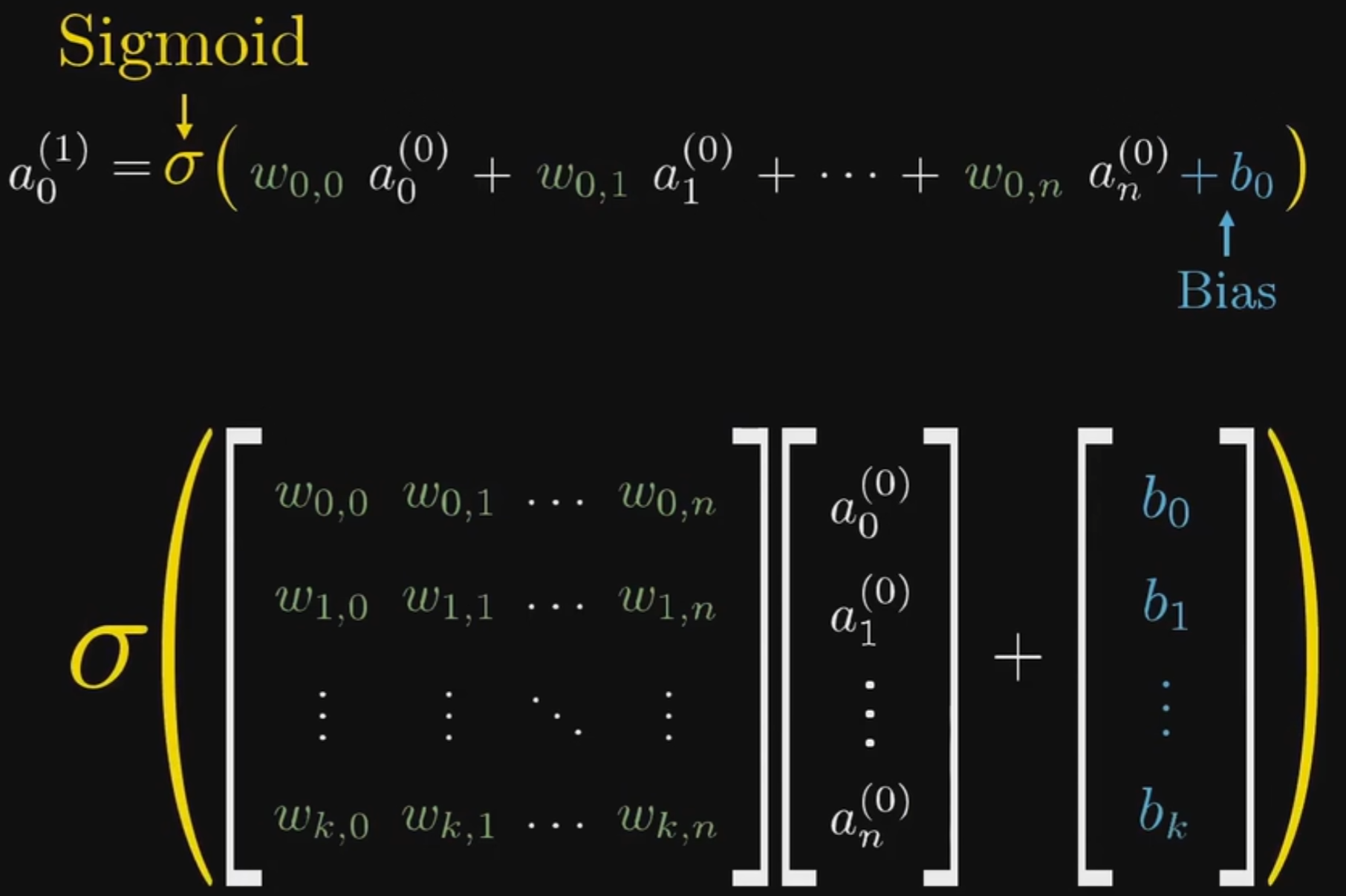 $$
前向传播函数:a^{(1)}=sigmoid(Wa^{0}+b)
$$
这里可以看出,此模型本质是一个以所有权重w以及偏置b为参数的函数,以784个神经元代表的图像为输入,以10个神经元代表的结果为输出。而训练模型的过程就是调节这些参数的过程。
$$
前向传播函数:a^{(1)}=sigmoid(Wa^{0}+b)
$$
这里可以看出,此模型本质是一个以所有权重w以及偏置b为参数的函数,以784个神经元代表的图像为输入,以10个神经元代表的结果为输出。而训练模型的过程就是调节这些参数的过程。
神经网络的训练-成本函数与反向传播
成本函数
在训练的最开始,我们会随机的初始化所有的权重w和偏置b,此时进行输入后得到的结果必定是错误的。因此需要定义一个函数来代表错误的程度,这里可以定义为如下图
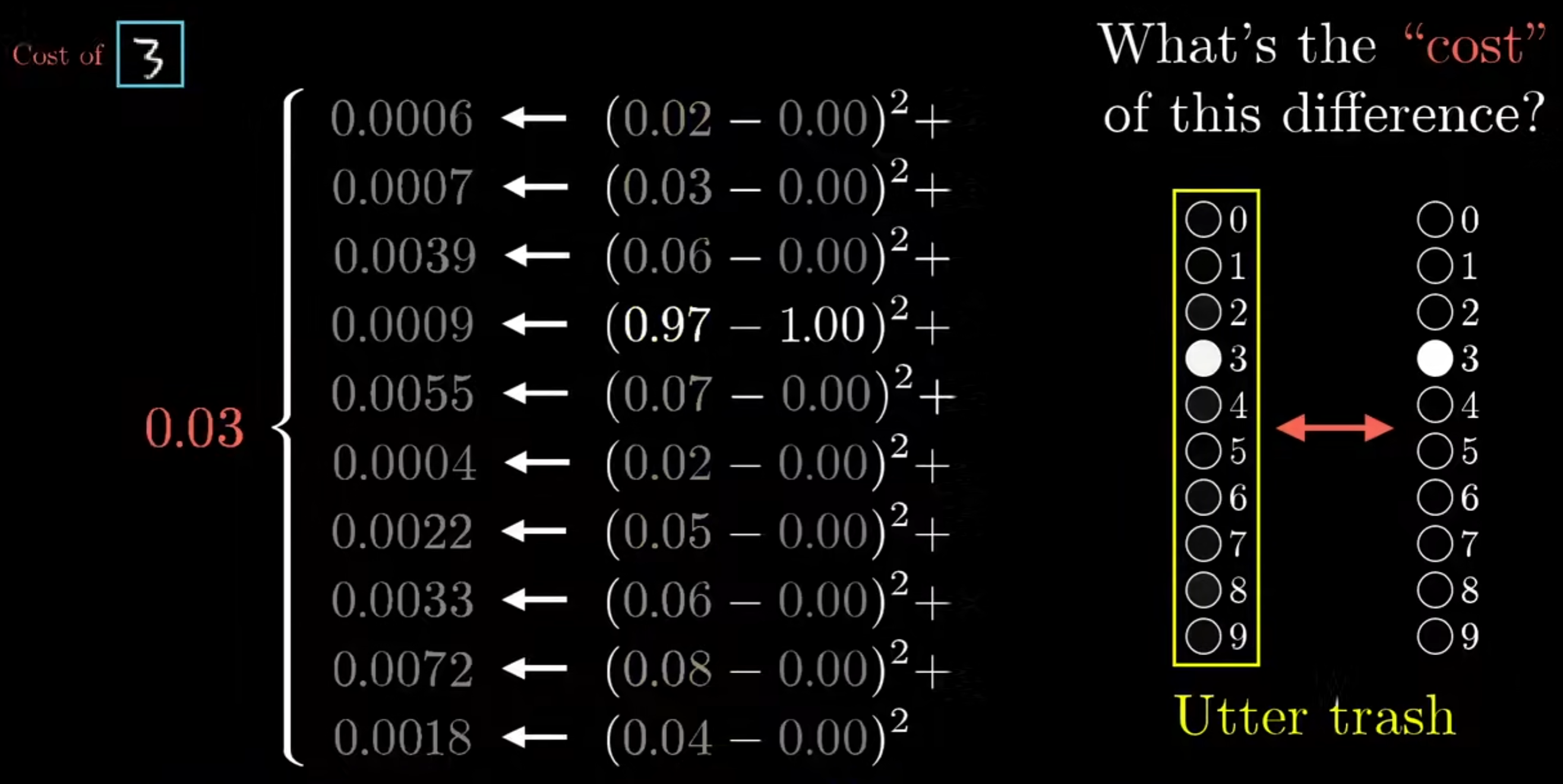 $$
即\sum(实际输出-应有输出)^2
$$
成本函数的定义不唯一,还会有其他方式定义的成本函数,依据具体情况而定。
$$
即\sum(实际输出-应有输出)^2
$$
成本函数的定义不唯一,还会有其他方式定义的成本函数,依据具体情况而定。
梯度下降
但是只知道错误的程度并不够,还需要知道如何调整所有的参数来获取更加正确的输出。
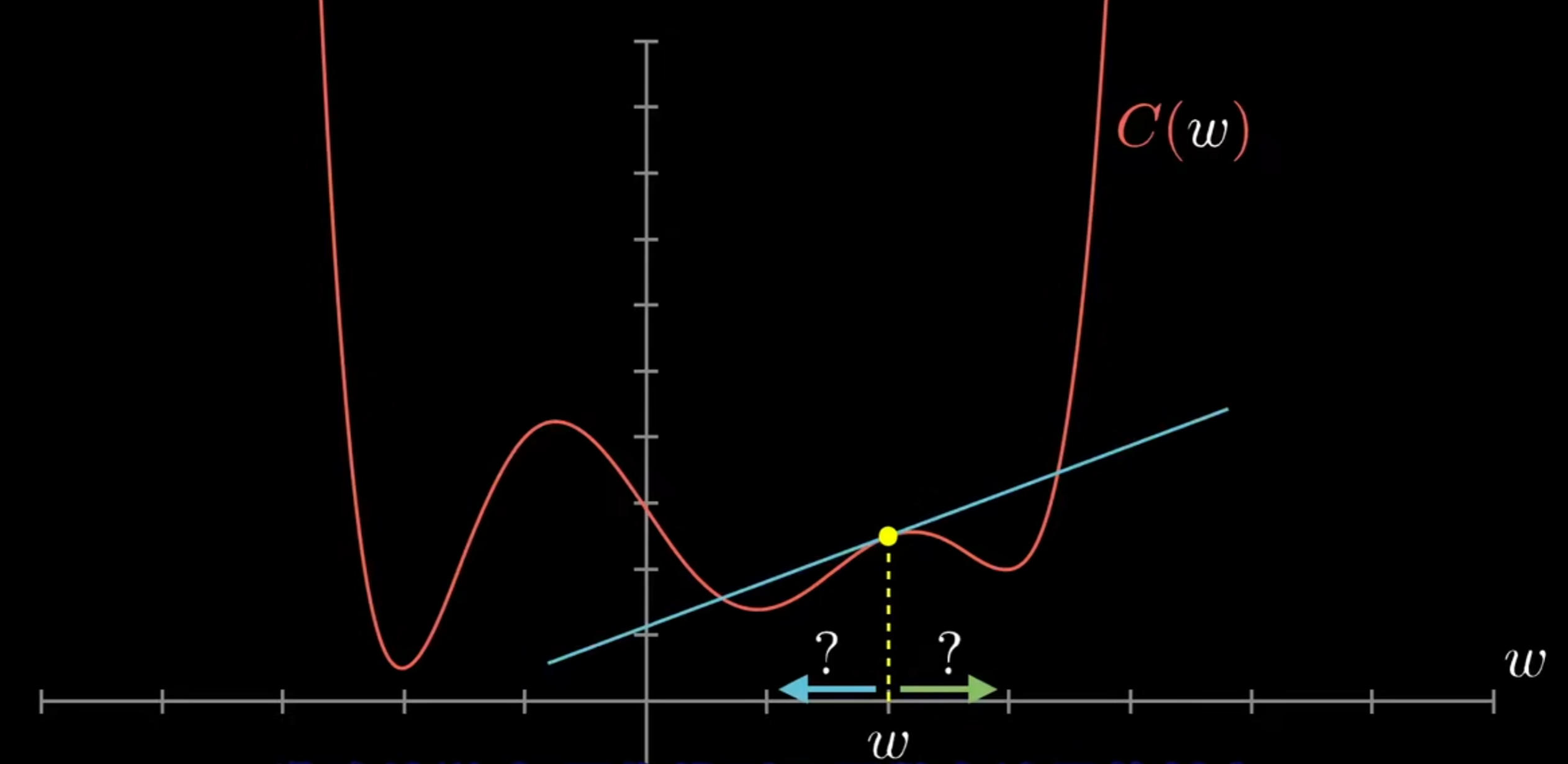
因此,可以先考虑一个一元函数如下图:
通过斜率可以清楚w调整的方向,并且当调整的数值与斜率的绝对值成正比时,w将最终收敛于函数的一个局部最小值。
回到成本函数,训练模型的过程其实就是努力最小化成本函数的过程,而这一过程其实并不复杂,想象一个结构十分简单的神经网络,每一层只有一个神经元,就可以得到下图:
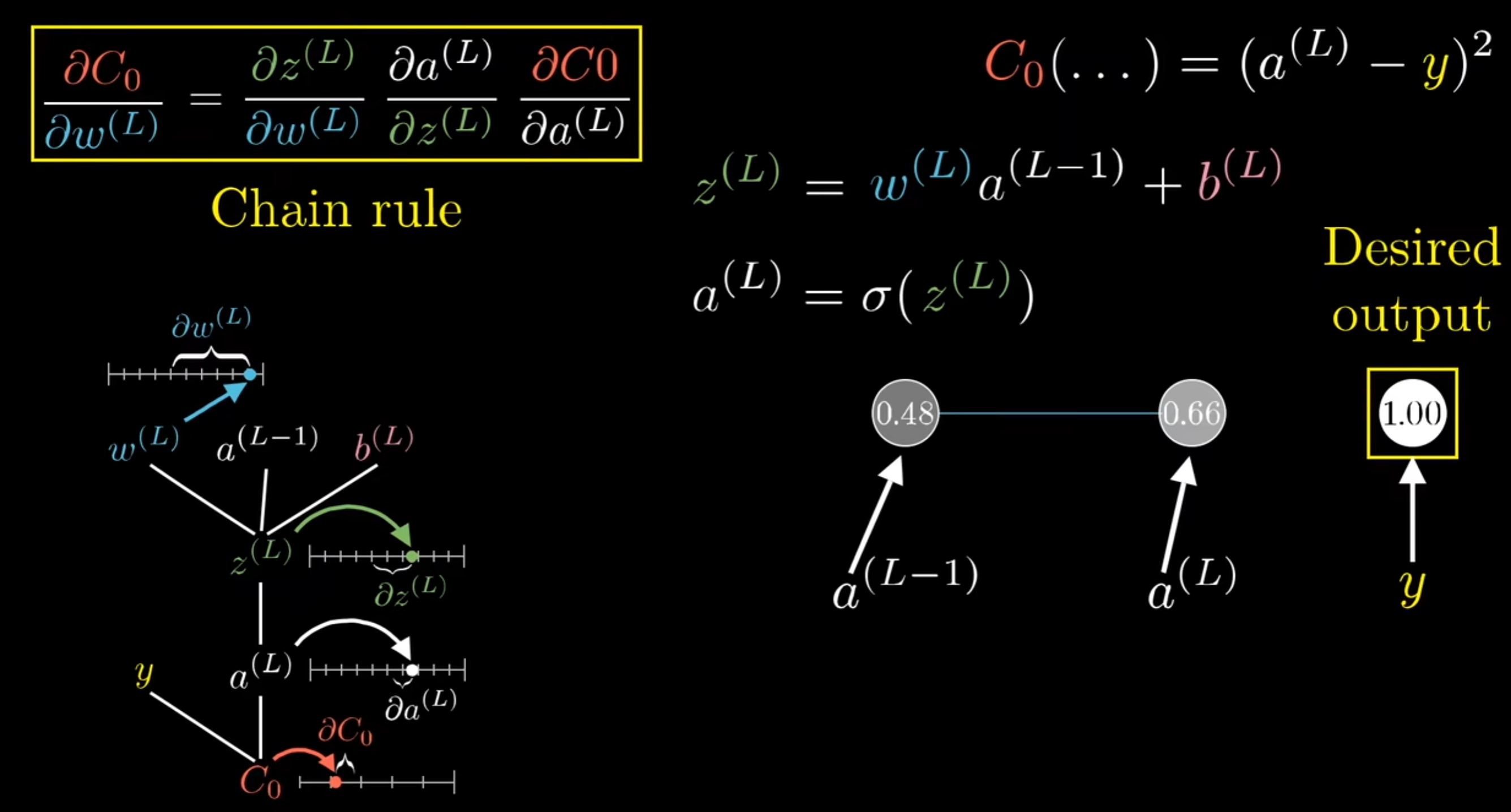 $$
Cost=(a^{(L)}-y)^2\
a^{(L)}=sigmoid(z^{(L)})\
z^{(L)}=w^{(L)}a^{(L-1)}+b^{(L)}\
其中因变量为Cost,自变量为w、b\
因此,梯度只需要分别对w、b求导即可(使用求导链式法则)\
\frac{\partial Cost}{\partial w^{(L)}}=\frac{\partial Cost}{\partial a^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial z^{(L)}}{\partial w^{(L)}}=[2(a^{(L)}-y)][sigmoid^{'}(z^{(L))})]a^{(L-1)}\
\frac{\partial Cost}{\partial b^{(L)}}=\frac{\partial Cost}{\partial a^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial z^{(L)}}{\partial b^{(L)}}=[2(a^{(L)}-y)][sigmoid^{'}(z^{(L))})]\
即可得到对于w、b的梯度向量
$$
获取梯度向量后,即可通过下列公式进行学习
$$
w{new}=w{old}-\eta\frac{\partial Cost}{\partial w_old}\
(\eta为学习率)
$$
而对于隐含层中的参数,同样可以基于链式法则求得梯度
$$
通过求取\frac{\partial Cost}{\partial a^{(L-1)}},再求\frac{\partial a^{(L-1)}}{\partial w^{(L-1)}}、\frac{\partial a^{(L-1)}}{\partial b^{(L-1)}}即可\以此类推可以求得所有w、b的梯度
$$
不断输入训练数据进行正向传播预测,计算成本函数,然后反向传播进行梯度下降,最终收敛至稳定,这就是神经网络训练的基本过程
$$
Cost=(a^{(L)}-y)^2\
a^{(L)}=sigmoid(z^{(L)})\
z^{(L)}=w^{(L)}a^{(L-1)}+b^{(L)}\
其中因变量为Cost,自变量为w、b\
因此,梯度只需要分别对w、b求导即可(使用求导链式法则)\
\frac{\partial Cost}{\partial w^{(L)}}=\frac{\partial Cost}{\partial a^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial z^{(L)}}{\partial w^{(L)}}=[2(a^{(L)}-y)][sigmoid^{'}(z^{(L))})]a^{(L-1)}\
\frac{\partial Cost}{\partial b^{(L)}}=\frac{\partial Cost}{\partial a^{(L)}}\frac{\partial a^{(L)}}{\partial z^{(L)}}\frac{\partial z^{(L)}}{\partial b^{(L)}}=[2(a^{(L)}-y)][sigmoid^{'}(z^{(L))})]\
即可得到对于w、b的梯度向量
$$
获取梯度向量后,即可通过下列公式进行学习
$$
w{new}=w{old}-\eta\frac{\partial Cost}{\partial w_old}\
(\eta为学习率)
$$
而对于隐含层中的参数,同样可以基于链式法则求得梯度
$$
通过求取\frac{\partial Cost}{\partial a^{(L-1)}},再求\frac{\partial a^{(L-1)}}{\partial w^{(L-1)}}、\frac{\partial a^{(L-1)}}{\partial b^{(L-1)}}即可\以此类推可以求得所有w、b的梯度
$$
不断输入训练数据进行正向传播预测,计算成本函数,然后反向传播进行梯度下降,最终收敛至稳定,这就是神经网络训练的基本过程
RNN(循环神经网络)结构与运行机制
RNN的前向传播
理解了基础的神经网络,循环神经网络其实就不难理解了。上图:
对于传统的神经网络,输入x1得到y1,输入x2得到y2。但是现实中很多任务需要将x1、x2关联,例如,输入“i”得到“我”,然后输入“like”得到“喜欢”;如果没有记住之前的输入“i”,那么“like的输出也可能是“像”。因此引入RNN模型,能够记忆之前的输入。
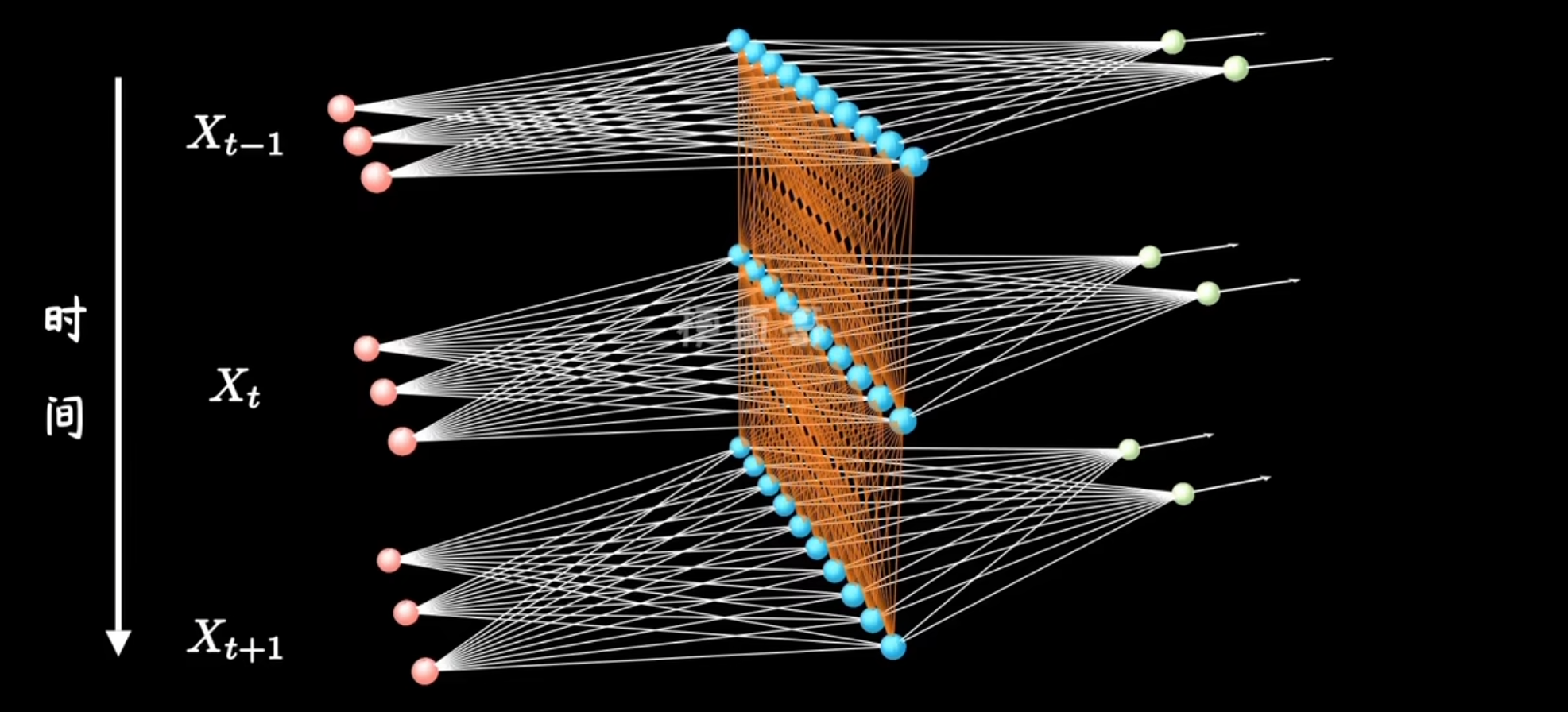
那么RNN是如何记忆的呢?如下图:
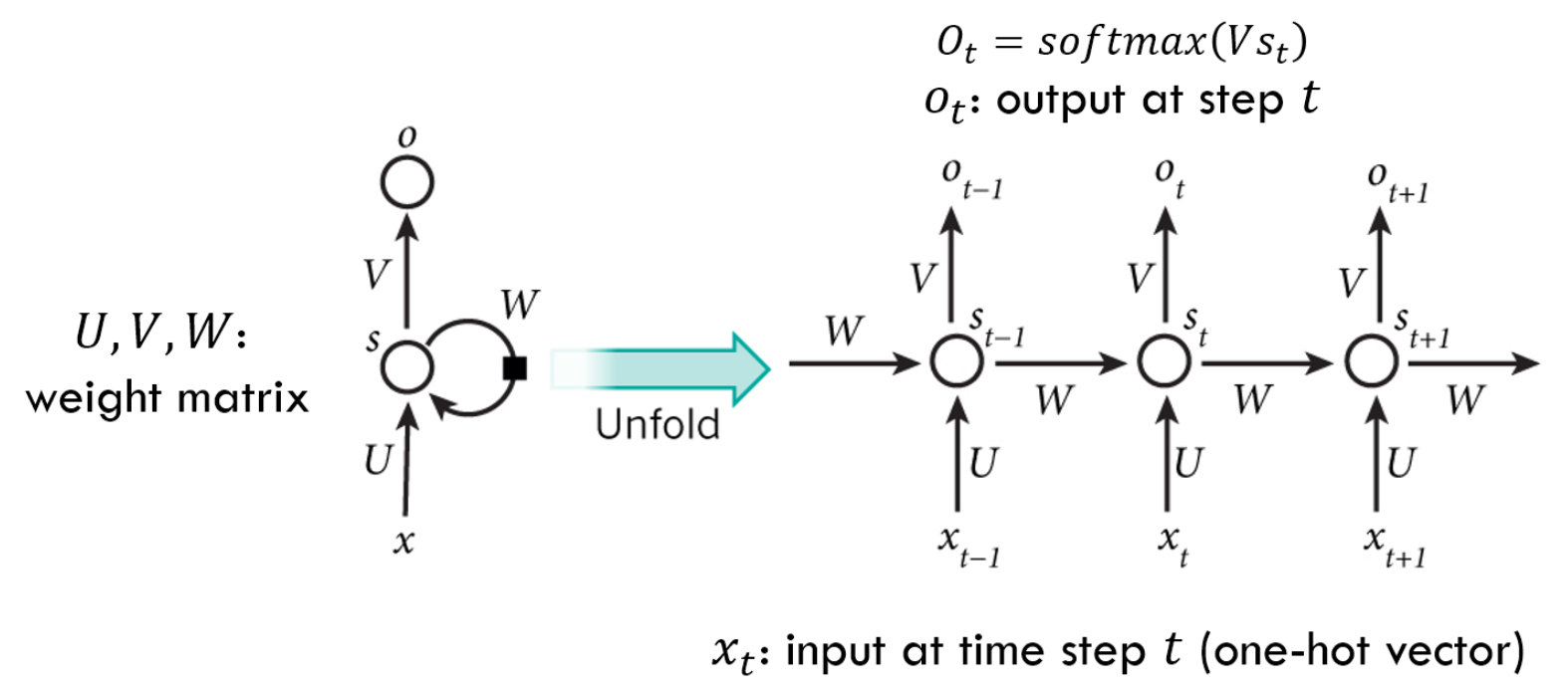
从左到右是时间的变化,可以看到随着时间的变化,有了不同的输入x,不同的输出o,以及不同的隐含层神经元值s $$ s{t}=Ux{t}+Ws_{t-1}\ o_t=Vs_t\ 因此,U、W、V为此模型的自变量参数 $$ 在传统神经网络中,隐含层的前向传播一般如下: $$ s=wx+b $$ 但在RNN中,隐含层的前向传播如下: $$ s_t=w_xx_t+wss{t-1}+b $$ 可以看到,这里的前向传播引入了上一时刻的隐含层神经元值,因此RNN具有了记忆的功能
RNN的反向传播
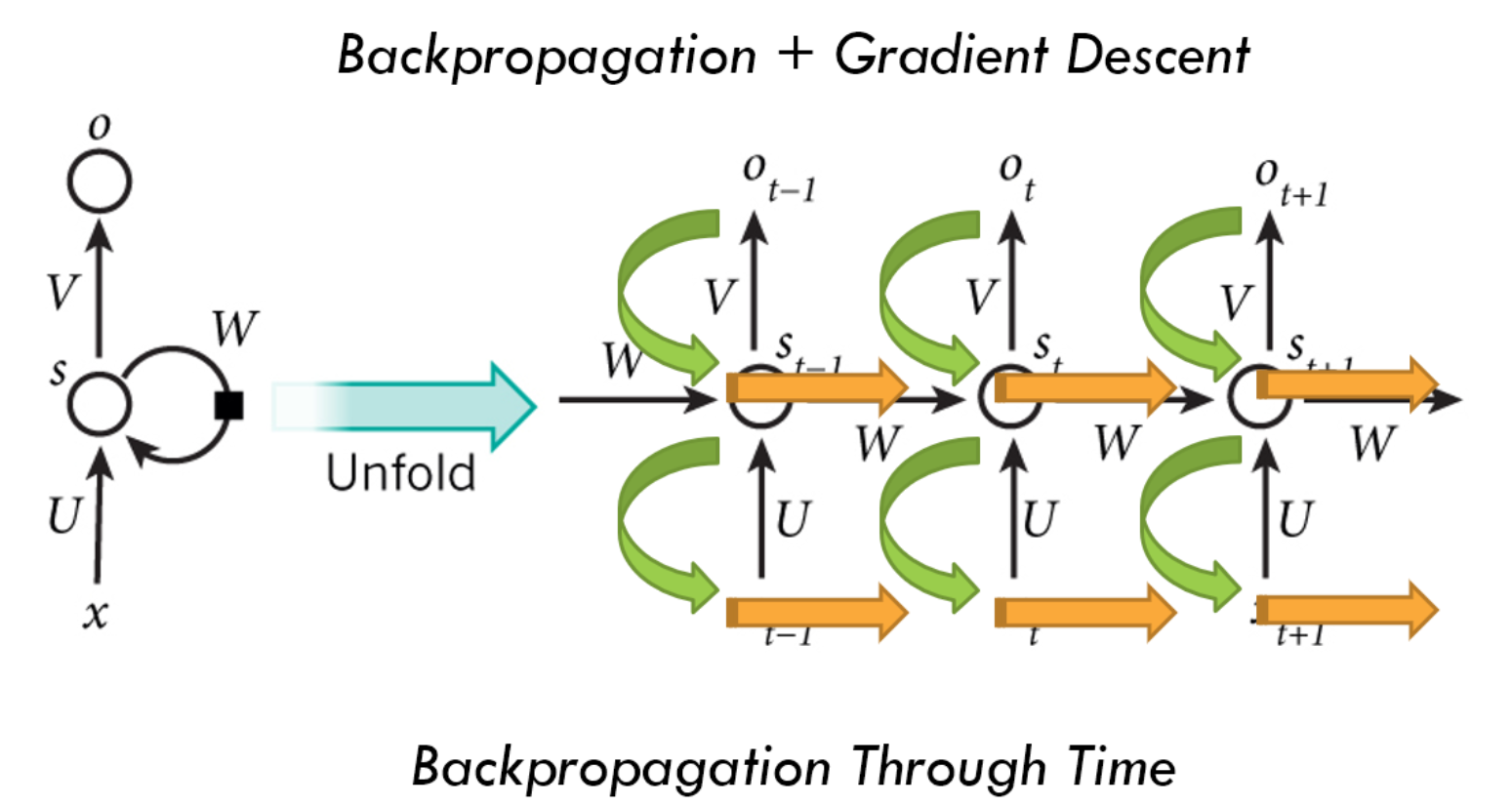
RNN也采用梯度下降反向传播的方法进行训练,而RNN的反向传播,自然也需要与时序有关。由于不同时序下模型使用的参数均为同一套参数,因此在不同时序下调整的参数也是相同的。训练过程如下图:
这里,成本函数的定义为不同时序下的输出对应的成本函数之和,即 $$ Cost=\sum^{T}_{t=0}Costt $$ 因此,在计算梯度下降时,可得到下列公式: $$ 当使用交叉熵函数为损失函数,激活函数使用softmax时\ \frac{\partial Cost}{\partial V}=\sum{t=0}^T\frac{\partial Costt}{\partial V}\ \frac{\partial Cost}{\partial W}=\sum{t=0}^T\sum_{k=0}^t\frac{\partial Cost_t}{\partial st}(\prod{j=k+1}^t\frac{\partial sj}{\partial s{j-1}})\frac{\partial sk}{\partial W}\ \frac{\partial Cost}{\partial U}=\sum{t=0}^T\sum_{k=0}^t\frac{\partial Cost_t}{\partial st}(\prod{j=k+1}^t\frac{\partial sj}{\partial s{j-1}})\frac{\partial s_k}{\partial U}\ $$ 可以看到对于U、W的梯度公式,包含了每个时序的损失值。这里个人没有细致推导(引用了网上的结果),记个TODO
- 推导反向传播公式
LSTM(长短期记忆网络)结构与运行机制
LSTM与普通RNN
继续观察刚才的公式,另一个值得注意的地方是,W和U的偏导的计算结果中都包含了一个连乘项。若连乘的项目数量不断增加,即t极大时,若$\frac{\partial s_{j-1}}{\partial s_j}$介于0~1之间,则连乘结果将无限接近于0,反之若大于1,则连乘结果将趋近正无穷。
这就是RNN不可避免的梯度消失*(Gradient Vanishing)和梯度爆炸(Gradient Explosion)*问题。
梯度消失/爆炸现象导致在梯度下降的计算中会出现极小/极大的梯度值,从而致使模型参数在训练中难以被继续更新。
因此,一般的RNN模型难以应对较长序列的输入,隐藏层节点的记忆能力有限,无法持续存储过去长远的信息。
针对这一问题,改进后的长短期记忆网络*(Long Short Term Memory Network)*横空出世。它通过增加一个并行的记忆通道,专门用于存储长期信息,称作*Cell State(可以理解为用于记忆的细胞)*。该通道通过累加运算消除了连乘带来的影响。也因此,LSTM在NLP任务中比RNN更为常用。
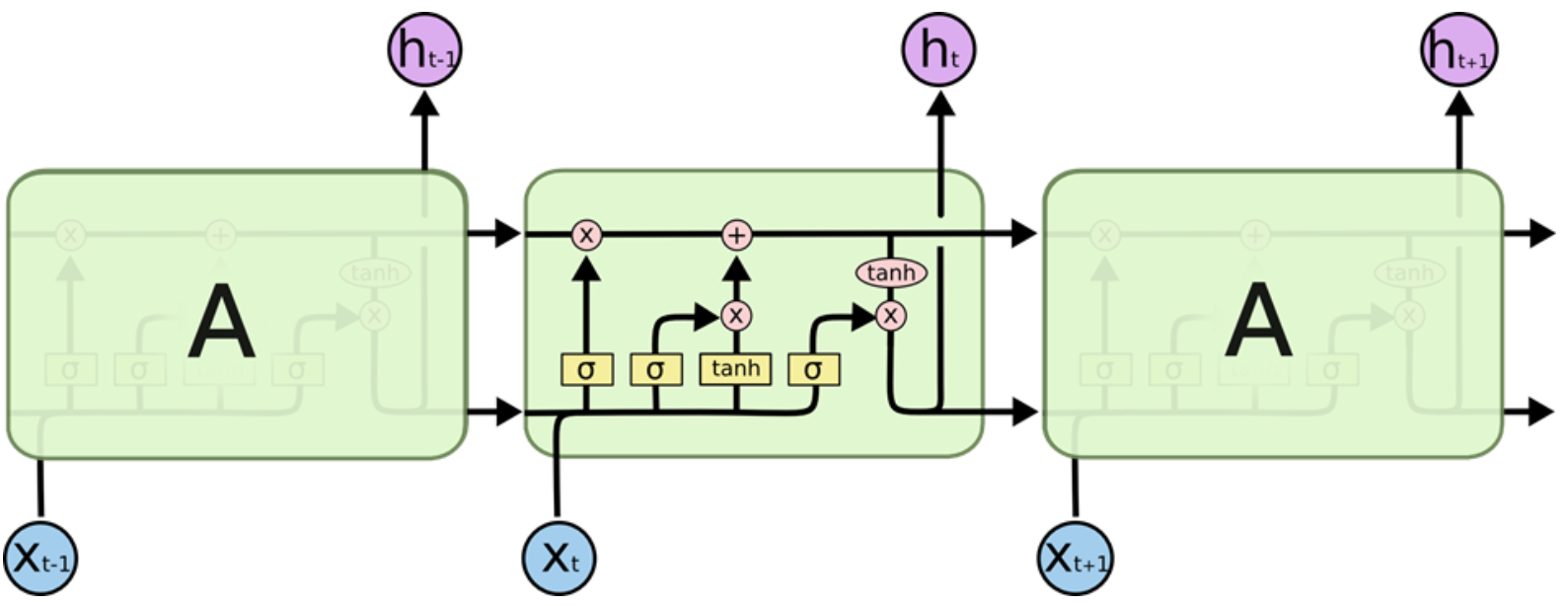
LSTM的结构如下图:
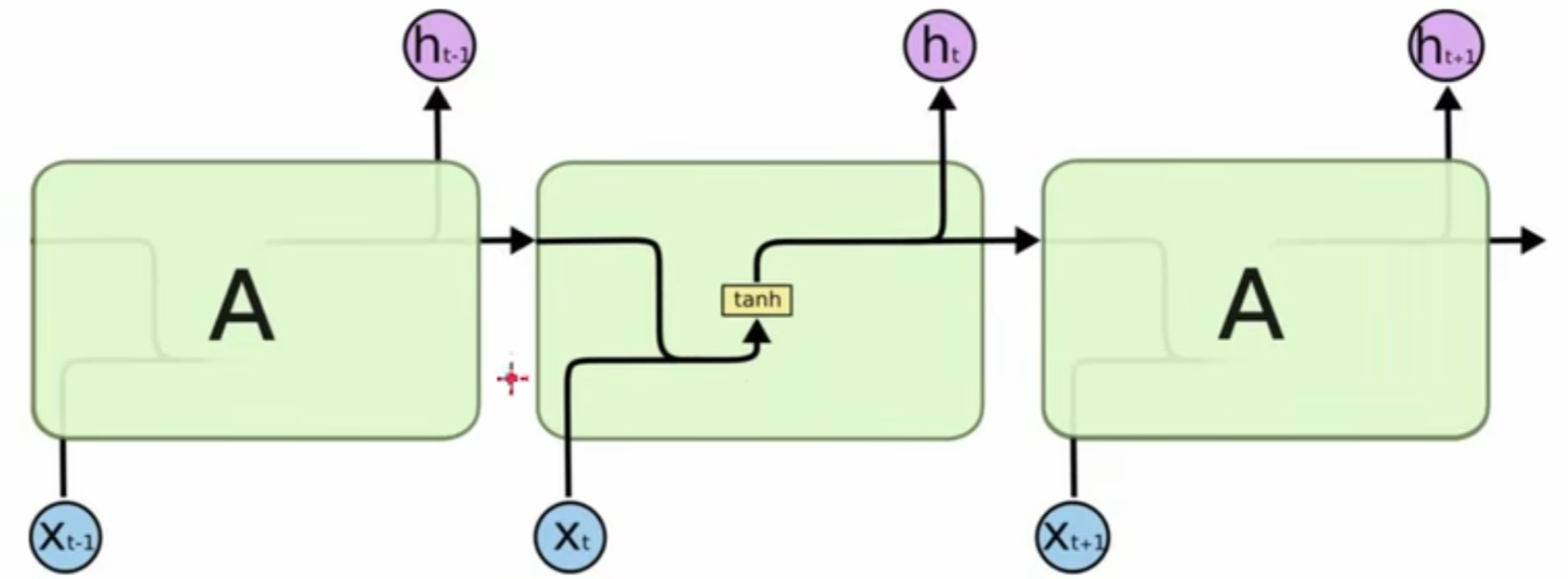
RNN的结构如下图:
可以看到,LSTM在不同的时序下多传输和保留了一类数据,即$c_t$,这就是LSTM新增的记忆通道:Cell State
LSTM的前向传播
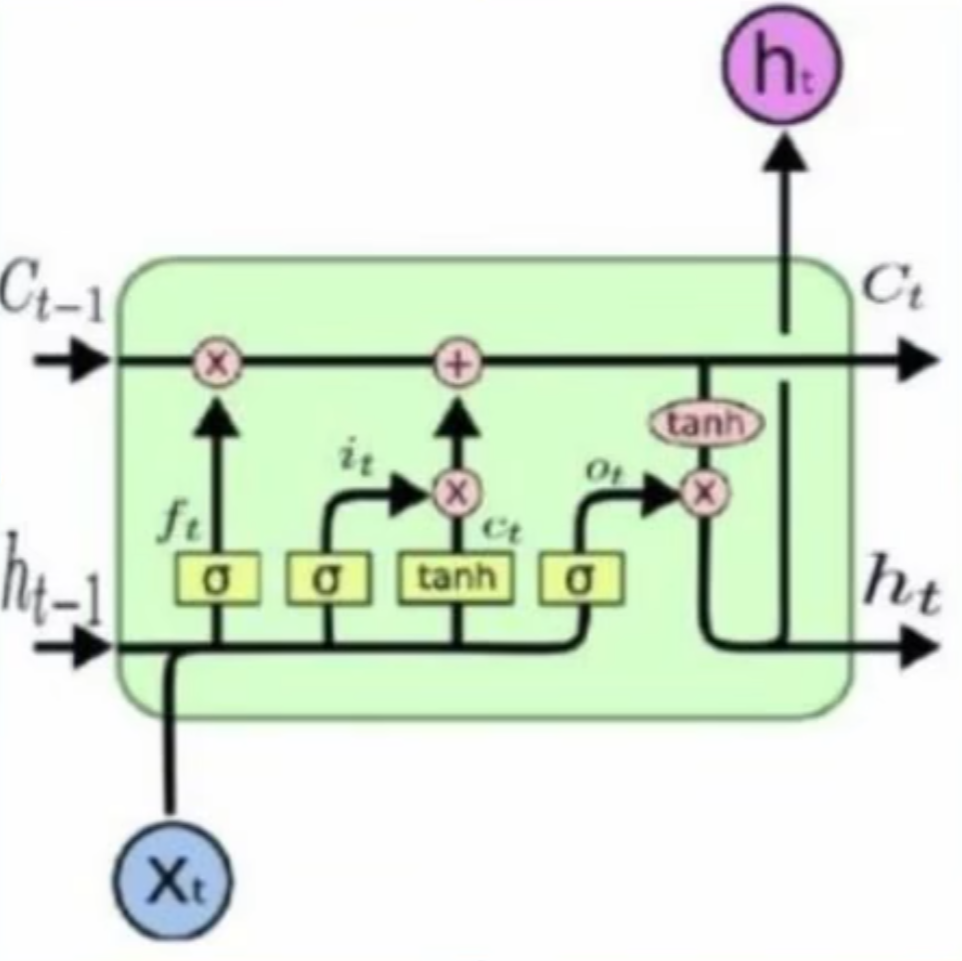 $$
遗忘因子:ft=sigmoid(W{xf}xt+W{hf}h_{t-1}+b_f)\
更新因子g_t:gt=tanh(W{xg}xt+W{hg}h_{t-1}+b_g)\
更新银子i_t:it=sigmoid(W{xi}xt+W{hi}h_{t-1}+b_i)\
合并长期记忆与短期记忆得到c_t:ct=c{t-1}*f_t+g_t*i_t\
输出因子o_t:ot=sigmoid(W{xo}xt+W{ho}h_{t-1}+b_o)\
输出因子m_t:m_t=tanh(c_t)\
合并长期记忆与短期记忆得到h_t:h_t=o_t*m_t\
最终该时序下输出为yt=W{yh}h_t+b_y
$$
这里具体的原理本人也没有进行推导,再记个TODO
$$
遗忘因子:ft=sigmoid(W{xf}xt+W{hf}h_{t-1}+b_f)\
更新因子g_t:gt=tanh(W{xg}xt+W{hg}h_{t-1}+b_g)\
更新银子i_t:it=sigmoid(W{xi}xt+W{hi}h_{t-1}+b_i)\
合并长期记忆与短期记忆得到c_t:ct=c{t-1}*f_t+g_t*i_t\
输出因子o_t:ot=sigmoid(W{xo}xt+W{ho}h_{t-1}+b_o)\
输出因子m_t:m_t=tanh(c_t)\
合并长期记忆与短期记忆得到h_t:h_t=o_t*m_t\
最终该时序下输出为yt=W{yh}h_t+b_y
$$
这里具体的原理本人也没有进行推导,再记个TODO
- 理解LSTM长短期记忆原理
LSTM模型预测文本序列实践
简单了解了原理,接下来通过预测文本来实践一下
如下是莎士比亚的一个剧本TXT文件:
数据预处理
首先读入数据
input_filepath = "./shakespeare.txt"
text = open(input_filepath, 'r').read()
可以输出看到结果如下
生成词库
vocab = sorted(set(text))
# set为一个无序不重复元素集,因此不重复地包含了text中所有的字符
生成由 字符->数字 的字典
char2idx = {char:idx for idx, char in enumerate(vocab)}
# 这里使用了python的简洁语法糖,以char:idx的形式对vocab进行遍历,并赋值到{}字典中
将词库转换为numpy中的array
idx2char = np.array(vocab)
# 为了后续能够提供给tensorflow作数据集
将数据加载到dataset中,并处理数据
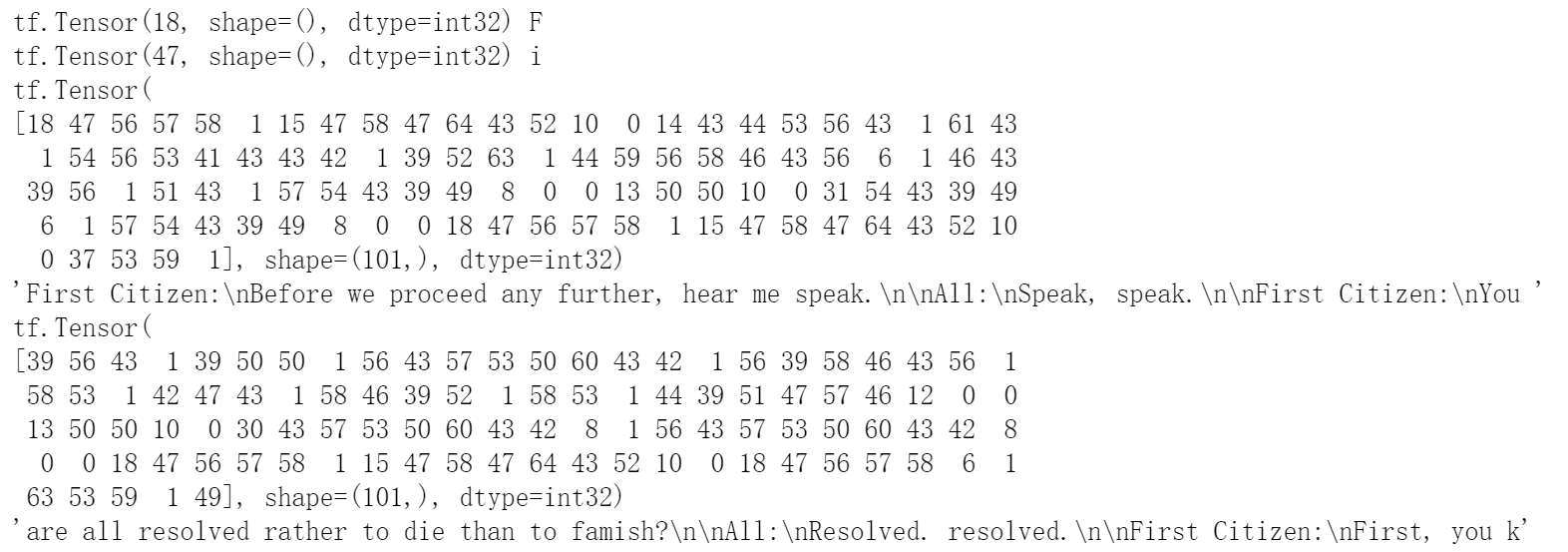
# 将array转换为tensor格式的数据
char_dataset = tf.data.Dataset.from_tensor_slices(text_as_int)
# 使用tensor的方法将数据集每个100个字符进行batch分序列
seq_length = 100
seq_dataset = char_dataset.batch(seq_length + 1, drop_remainder = True)
# 这样就可以通过输入第1到100个字符,让模型预测第101个字符来训练
将数据分割成输入和输出两个部分
def split_input_target(id_text):
# 将序列作如下变化 abcde -> abcd, bcde
return id_text[0:-1], id_text[1:]
seq_dataset = seq_dataset.map(split_input_target)
# 这里获得了模型的输入与预期输出,即输入第1到100个字符,让模型预测输出第2到101个字符
打乱数据,batch分组,batch_size=64
batch_size = 64
buffer_size = 10000
# 将数据打乱顺序并分组,分组主要是为了防止对单一样本进行梯度下降,导致长时间无法找到对于全局来说最优的梯度,分组可以保证始终取部分样本的梯度均值
seq_dataset = seq_dataset.shuffle(buffer_size).batch(batch_size, drop_remainder=True)
构造模型
定义模型常量
vocab_size = len(vocab)# 词库大小,即此位置下的字符为词库中某字符的概率是多少
embedding_dim = 256
rnn_units = 1024
定义model模型
inputs = keras.Input(batch_input_shape=(batch_size,None))
# 这里的size中的None代表可能为任何正整数,因此后续的输入长度可以为任意长度
outputs = keras.layers.Embedding(vocab_size, embedding_dim)(inputs)
# 这里是一个嵌入层,用于将词的下标(这里是字符在词库中的下标)映射到词向量上(一个数据映射到一个向量上),这里我认为可以理解为变为one-hot编码(one-hot编码十分稀疏,embedding会更稠密一些)
outputs = keras.layers.LSTM(units = rnn_units,stateful = True,recurrent_initializer='glorot_uniform',return_sequences = True)(outputs)
# keras库封装好的LSTM层
outputs = keras.layers.Dense(vocab_size)(outputs)
# 输出层
model = Model(inputs, outputs)
model.summary()
定义损失函数和优化器
# 定义优化器和自定义损失函数
def loss(labels, logits):
return keras.losses.sparse_categorical_crossentropy(labels, logits, from_logits=True)
# 这里是一个交叉熵函数
model.compile(optimizer = 'adam', loss = loss)
其他交叉熵函数及其区别和应用场景可以看这里:传送门
训练模型
checkpoints,顾名思义,保存检查点可以多次训练
output_dir = "./text_generation_lstm3_checkpoints"
if not os.path.exists(output_dir):
os.mkdir(output_dir)
checkpoint_prefix = os.path.join(output_dir, 'ckpt_{epoch}')
checkpoint_callback = keras.callbacks.ModelCheckpoint(filepath = checkpoint_prefix,save_weights_only = True)
开始训练
epochs = 100
history = model.fit(seq_dataset, epochs = epochs,callbacks = [checkpoint_callback])
# 会自动找到最近保存的变量文件
new_checkpoint = tf.train.latest_checkpoint(output_dir)
使用模型进行预测
加载模型
# Model 定义预测模型
inputs = keras.Input(batch_input_shape=(1,None))
print(inputs.shape)
outputs = keras.layers.Embedding(vocab_size, embedding_dim)(inputs)
print(outputs.shape)
outputs = keras.layers.LSTM(units = rnn_units,stateful = True,recurrent_initializer='glorot_uniform',
return_sequences = True)(outputs)
print(outputs.shape)
outputs = keras.layers.Dense(vocab_size)(outputs)
print(outputs.shape)
model2 = Model(inputs, outputs)
model2.load_weights(tf.train.latest_checkpoint(output_dir))
model2.summary()
预测模型做预测
def generate_text(model, start_string, num_generate = 1000):
input_eval = [char2idx[ch] for ch in start_string]
input_eval = tf.expand_dims(input_eval, 0)
text_generated = []
model.reset_states()
for _ in range(num_generate):
# 输入进入模型,得到预测
predictions = model(input_eval)
# 去掉一维的结构
predictions = tf.squeeze(predictions, 0)
# 根据此位置的词库中不同字符的可能性进行采样,获得预测出的字符
predicted_id = tf.random.categorical(predictions, num_samples = 1)[-1, 0].numpy()
# 将预测出的字符最后一位添加到已经生成的字符串末尾
text_generated.append(idx2char[predicted_id])
# 将预测出的字符最后一位作为输入再次输入到模型中预测
input_eval = tf.expand_dims([predicted_id], 0)
return start_string + ''.join(text_generated)
new_text = generate_text(model2, "Al",10)
print(new_text)
这里理论上应该还有一个采样函数,用于自定义在采样时的偏好,时间关系这里就不多写了,有兴趣可以参考采样策略
总结
最终训练得到的模型一共进行了100轮训练,最终得到的效果对单词的预测完整度尚可,但句子较少构成语义。同时keras的封装带来方便的同时也掩盖了很多算法的实现,之后还是需要继续完善这里的理解。